Fronteira Eficiente na prática - Como otimizar a alocação de ações num portfólio? Parte 3
Fala pessoal!
No post passado expliquei o que era o algoritmo de Otimização por Média-Variância, e como o seu cálculo para todas as combinações possíveis de portfólio dado um conjunto de ações gerava a Fronteira Eficiente.
Nesse post, utilizaremos os conceitos introduzidos nos dois últimos posts da série para gerar portfólios reais com base em ações escolhidas anteriormente.
Já vimos que a Teoria Moderna do Portfólio nos diz como investidores podem construir portfólios que minimizam o risco dado um nível esperado de retorno. Agora vamos ver como isso funciona na prática, criando portfólios artificiais através de simulações para diferentes níveis de retornos esperados.
Para realizar as simulações, precisamos escolher algumas ações. Para facilitar nossa vida, resolvi usar um conjunto de ações que foi utilizada na série anterior aqui do site, “Comparação de Performance de Carteiras”. Nessa série, usei três critérios diferentes para selecionar boas ações para compor um portfólio. No primeiro post dela, usei o critério de média/desvio-padrão. As ações escolhidas foram: ABEV3, EQTL3, LREN3, CIEL3, RADL3, MDIA3, WEGE3, EZTC3 e FLRY3.
Nele, a minha maior preocupação era de encontrar ações para compor o portfólio, e nem tanto os pesos exatos que cada ação iria receber, que é exatamente o intuito desse post que vocês estão lendo.
Os dados das ações foram obtidos no Yahoo Finance, e correspondem aos pregões do início de 2012 até novembro do ano passado.
O código em Python que usei para realizar as simulações pode ser encontrado na minha página do Github, que você pode acessar aqui.
Utilizando o método de Monte Carlo, criei duzentos mil portfólios artificiais que depois foram plotados para identificar a presença da fronteira eficiente.
- Retornos esperados para cada papel;
- Volatilidade de cada papel;
- Covariância entre as ações;
- Retorno alvo que queremos obter.
Nesse caso, nós possuímos os retornos e volatilidade médios de cada ação ao longo desse período de 2012 a 2018, e com isso calculamos a covariância entre as ações.
Por fim, testamos para cada uma desses duzentos mil portfólios artificiais um nível diferente de retorno alvo.
Abaixo você vê os cinco portfólios com o maior retorno esperado, em ordem decrescente:

O portfólio com o maior retorno (28,7%) é o que tem a seguinte composição:

Os portfólios simulados que eu obtive são mostrados no gráfico abaixo:

Traçando uma curva para visualizar melhor a fronteira eficiente:
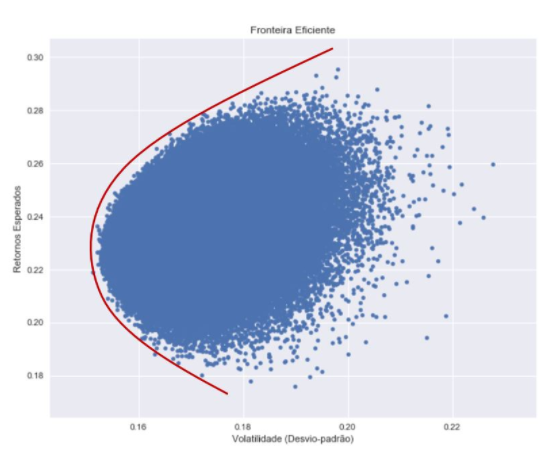
Cada ponto sobre a fronteira eficiente representa uma combinação ótima de ações que maximiza o retorno esperado para um dado nível de risco.
Com isso provamos a viabilidade de se usar o algoritmo de Otimização por Média-Variância para a simulação de portfólios. Encontramos também um portfólio que maximiza o retorno, dentro daquele conjunto de ações que tínhamos no começo, lembrando que esse não é o portfólio que minimiza a volatilidade, apenas otimiza o retorno.
E por fim, isso não é uma recomendação de investimento! Meu propósito aqui é muito mais de apresentar os conceitos e os resultados das simulações do que criar uma carteira que seja usada na prática, muito embora eu utilize vários desses conceitos na vida real.
No próximo e último post dessa série, vou mostrar algumas métricas que podemos obter com a Fronteira Eficiente, e como determinar o portfólio que minimiza o risco. Até lá!
#ações #efficientfrontier #fronteiraeficiente #mvo #MPT #Markowitz #volatilidade #retornos #OMV #Python #otmimização
